Bahas Soal Matematika   »   Pertidaksamaan Matematika   ›  

Semua nilai \(x\) yang memenuhi \( \sqrt{x+10} - \sqrt{x+2} > 2 \) adalah…

1. \( -2 \leq x < -1 \)
2. \( x > 1 \)
3. \( -\frac{3}{2} \leq x < -1 \)
4. \( x > 2 \)
5. \( -1 < x < 6 \)

(SBMPTN 2014)

Pembahasan:

Untuk menyelesaikan pertidaksamaan bentuk akar di atas, ada beberapa langkah yang perlu kita lakukan.

Langkah pertama: Selesaikan pertidaksamaan bentuk akar tersebut dengan menyamakan ruas kiri dan kanan, kemudian dikuadratkan. Kita peroleh berikut ini:

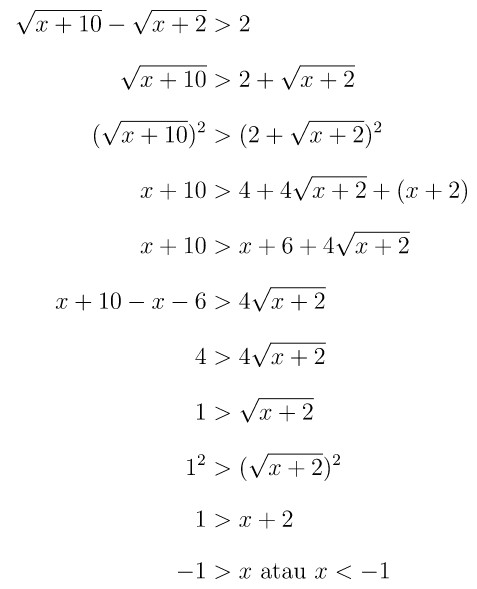
Langkah kedua: Carilah nilai \(x\) yang memenuhi atau membuat \( \sqrt{x+10} \) terdefinisi. Agar \( \sqrt{x+10} \) terdefinisi maka nilai \(x\) yang memenuhi, yaitu:

Langkah ketiga: Lakukan hal yang sama seperti pada Langkah Kedua di atas untuk mencari nilai \(x\) yang memenuhi atau membuat \( \sqrt{x+2} \) terdefinisi. Kita peroleh berikut ini:

Irisan ketiga nilai \(x\) yang memenuhi pada pertidaksamaan di atas adalah himpunan penyelesaian dari pertidaksamaan bentuk akar yang diberikan dalam soal ini. Jika digambarkan, kita peroleh berikut ini:

Dari gambar di atas, himpunan penyelesaiannya adalah \( -2 \leq x < -1 \).

Jawaban A.